From PPO to FPO- Flow Models for Better Policies

• Vrushtee Gaikwad
• Tirth Gada

Project report github:

Robot-learning(EKLAVYA 2025)

Lerobot-sim2real FPO implementation:

Lerobot-sim2real fork with FPO implementation

From PPO to FPO: Flow Models for Better Policies

Abstract

Proximal Policy Optimization (PPO) is one of the most popular reinforcement learning algorithms, widely adopted for its stability and efficiency. However, PPO’s reliance on Gaussian policies limits its expressiveness, particularly for multimodal and high-dimensional action spaces common in robotic manipulation tasks. Flow Policy Optimization (FPO) combines Conditional Flow Matching (CFM) with on-policy reinforcement learning to overcome these limitations, enabling expressive policy learning without sacrificing stability. This note outlines the motivation for transitioning from PPO to FPO, explains the underlying mathematical framework (including ELBO derivations), and highlights advantages for sim-to-real robotics pipelines.

Introduction

When discussing reinforcement learning algorithms, Proximal Policy Optimization (PPO) often tops the list. However, there are some disadvantages to using PPO in RL implementations for hardware manipulation tasks. Gaussian policies can lack the expressiveness needed for multimodal and high-dimensional action spaces. In such cases, we can consider alternative algorithms like Flow Policy Optimization (FPO), which allow us to train expressive flow-based policies and design reward functions with greater flexibility.

What is PPO?

PPO is a reinforcement learning algorithm, which means it tries to find the best policy (set of actions) that will maximize the agent’s expected cumulative reward. It does this by using a technique called policy gradient, which calculates the gradient of the expected reward with respect to the policy parameters, and then updates the parameters in the direction that improves the policy.

Key points:

1. Goal: Maximize the total reward (gradient ascent).
2. Robustness: Parameters and hyperparameters are tuned to make the policy stable.
3. Stochastic sampling: PPO samples rollouts from the environment to estimate gradients.
4. First-order optimization: Only gradients are used (no second derivatives).
5. On-policy algorithm: Uses data collected from the current policy.
6. Clipped surrogate objective: Keeps policy updates within a trust region by clipping the probability ratio between (1 - ε) and (1 + ε).

Mathematically, the PPO clipped objective is:

\[L^{\mathrm{CLIP}}(\theta) = \mathbb{E}_t \Big[ \min\big( r_t(\theta) \,\hat{A}_t,\; \mathrm{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon)\,\hat{A}_t \big) \Big]\]

where

\[r_t(\theta) = \frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_{\mathrm{old}}}(a_t\mid s_t)}\]

and $\hat{A}_t$ is the advantage estimate.

Why FPO?

So when we talk about reinforcement learning algorithms PPO tops the list.But there are definitely a few disadvantages to the idea of using PPO in rl implementations. Gaussian policies lack implementations and expressiveness required for multimodal and high dimensional action workspaces. Here, we think about alternative algorithms like FPO which help us train RL, expressive flow policies and write reward functions for better expressivity.

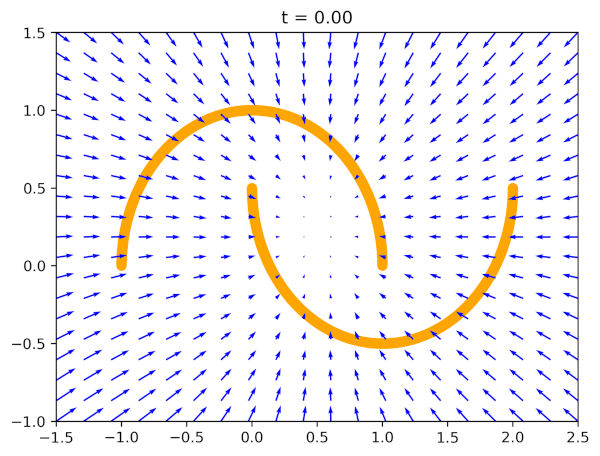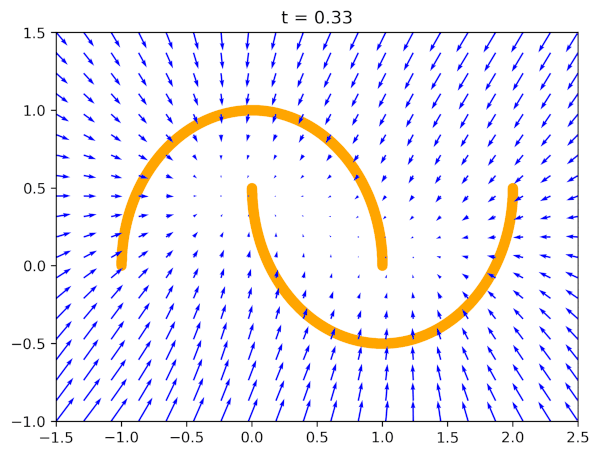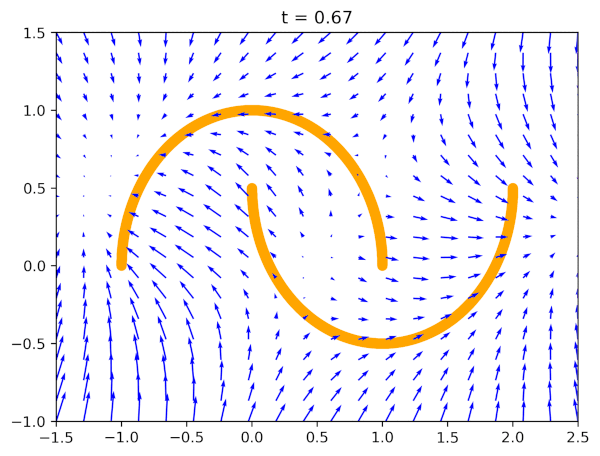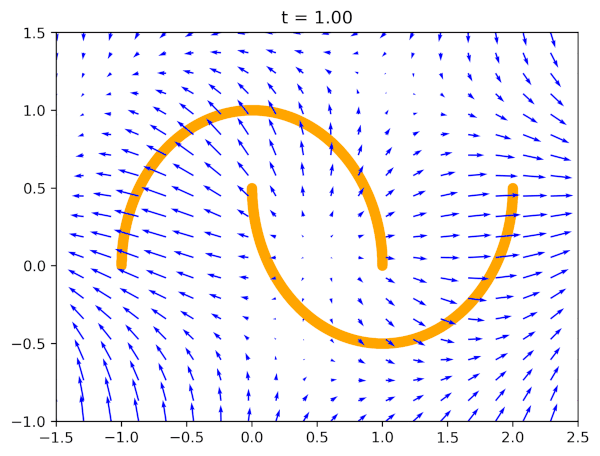
Flow Matching

Flow Matching is a method for transforming noise into the target data distribution through a continuous vector field.

Two common trajectory types:

1. Diffusion-style paths: smooth, possibly curved trajectories.
2. Optimal transport (OT) displacement paths: straight-line (displacement) trajectories under a quadratic cost.

Process:

1. Sample an intermediate state at a random time $t$.
2. Given known start (noise) and end (data) points, compute the instantaneous target velocity analytically from the chosen path definition.
3. Train a network to predict these velocity vectors.
4. Integrate the learned vector field from noise to the data distribution.

Conditional Flow Matching (CFM) conditions the flow on inputs (e.g., observations or states) and works well for visual and control tasks.

Flow Policy Optimization (FPO)

FPO combines Flow Matching with on-policy RL (e.g., PPO) to redirect probability flow toward high-reward actions.
It leverages flow expressiveness for multimodal action distributions while keeping on-policy stability.

Key features of FPO

Conditional Flow Matching (CFM) objective

1. The CFM loss measures the squared difference between the network-predicted instantaneous velocity and the true velocity defined by the path.
2. It avoids computing complex log-likelihoods directly.
3. Practically, it helps map noisy actions into smooth, robust action trajectories.

Monte Carlo sampling

1. At each training step, sample random noise-action pairs.
2. Compute CFM loss and advantage estimates (e.g., GAE) per sample and average to reduce variance.
3. The Monte Carlo averaging improves stability.

FPO surrogate objective

1. Uses ELBO (Evidence Lower Bound) as a surrogate for log-likelihood to obtain tractable likelihood proxies.
2. A ratio of ELBO exponents between new and old policies approximates the policy probability ratio.
3. Flow models are expressive but computing exact log-likelihoods requires log-determinants of Jacobians, which is expensive in high dimensions.
4. FPO mitigates this by predicting vector fields and using advantage-weighted objectives.

Training and inference

Training:

1. Sample a random interpolation point between noise $z$ and data $a$.
2. Compute the direction that pushes the sample toward the data.
3. Train the model to predict that direction (CFM loss) alongside RL objectives.

Inference:

• Integrate the learned vector field using ODE solvers or iterative (diffusion-like) steps to obtain actions.

ELBO derivation for Flow Policy Optimization

In probabilistic modeling, the Evidence Lower Bound (ELBO) is a surrogate for the log-likelihood:

\[\log p_\theta(a|s) \ge E_{q_\phi(z|a,s)} \left[ \log p_\theta(a|z,s) \right] - KL\left( q_\phi(z|a,s) \| p(z) \right),\]

where $a$ is the action, $s$ the state, $z$ a latent variable, $p(z)$ the prior, and $q_\phi$ the variational posterior.

ELBO for invertible flow models

For bijective flows we can write the exact log-density via change of variables:

\[\log p_\theta(a|s) = \log p_z\left(f_\theta^{-1}(a,s)\right) + \log\left|\det \frac{\partial f_\theta^{-1}(a,s)}{\partial a}\right|.\]

The second term (log-determinant of the Jacobian) captures volume change and is the expensive component for high-dimensional actions.

FPO ratio for surrogate objective

PPO uses the probability ratio

\[r_t(\theta) = \frac{\pi_\theta(a_t\mid s_t)}{\pi_{\theta_\mathrm{old}}(a_t\mid s_t)}.\]

FPO approximates this using ELBO-based proxies:

\[r_t^{FPO}(\theta) \approx \frac{\exp(ELBO_\theta(a_t,s_t))}{\exp(ELBO_{\theta_{old}}(a_t,s_t))},\]

which avoids exact log-determinant computations every update.

Advantage-weighted conditional flow matching loss

Combine clipped surrogate RL objective with the CFM regularizer:

FPO Objective:

$L_{FPO}(\theta) = \mathbb{E}_t\left[ \min\left( r_t^{FPO}(\theta) \hat{A}_t, \text{clip}(r_t^{FPO}(\theta),1-\epsilon,1+\epsilon)\hat{A}_t \right) \right]$

With CFM regularization:

$L_{total}(\theta) = L_{FPO}(\theta) + \lambda \cdot L_{CFM}(\theta)$

where $L_{CFM}$ is the conditional flow matching loss and $\lambda$ balances stability vs expressiveness.

Why FPO is better for sim-to-real robotics

1. Reality-Sim gap mitigation. In sim-to-real transfer, the “training set” is the set of rollouts from simulation, but the deployment environment is real-world physics..Flow matching interprets this as learning probability transport maps from a simple prior to actions conditioned on observations. When that map is trained on a variety of simulated conditions such as lighting issues , the learned flow naturally routes probability mass toward action trajectories that remain valid across multiple domains.
2. Multi-modal action generation. In robotics tasks,usually there’s more than one “right” answer .The same manipulation task may be performed with a different trajectory or action chunks. A Gaussian policy is like a hill with one peak which encapsulates only one single strategy .Flow based policies can form multiple peaks each representing a viable approach .The flow can split into several streams enabling the robot to switch between strategies on the fly depending on the environment.
3. Balanced expressiveness & efficiency. Using CFM and ELBO proxies reduces costly exact likelihood evaluations.
4. Stable policy optimization & safety. FPO replaces exact likelihood maximization with advantage-weighted conditional flow matching, keeping updates bounded in the same way PPO’s trust-region clipping does. This preserves training stability while simplifying the objective. For real-world robots, that stability translates into predictable, gradual policy changes, avoiding the erratic shifts that can cause unsafe motions.

Conclusion

Flow Policy Optimization (FPO) combines flow-based generative modeling and on-policy RL to produce expressive, stable policies—particularly suited to robotic manipulation and sim-to-real transfer.

References

1. Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017). Proximal Policy Optimization Algorithms. arXiv preprint arXiv:1707.06347. https://arxiv.org/abs/1707.06347

2. McAllister, D., Ge, S., Yi, B., Kim, C. M., Weber, E., Choi, H., Feng, H., & Kanazawa, A. (2024). Flow Policy Optimization. arXiv preprint arXiv:2507.21053. https://arxiv.org/abs/2507.21053

3. Flow Matching Policy Gradients Blog. https://flowreinforce.github.io - Interactive demonstrations and detailed explanations of FPO implementation.

4. Lipman, Y., Chen, R.T.Q., Ben-Hamu, H., Nickel, M., & Le, M. (2023). Flow Matching for Generative Modeling. arXiv preprint arXiv:2210.02747. https://arxiv.org/pdf/2210.02747