The Society of Robotics and Automation is a society for VJTI students. As the name suggests, we deal with Robotics, Machine Vision and Automation
Done with the initial step...now what!?
After completing the simulation of basic systems like simple pendulum, spring-mass and complex pulley on MATLAB, we have moved ahead to simulate the Rotary Inverted Pendulum system.
Starting with the simulation
Our first step to achieve the simulation was to derive the Langrangian equations so that we could define the functions of the state vectors. So, we referred to some papers for the equations as manually deriving it is difficult. For this system, the state vectors are θ$_0$ and θ$_1$.
The Langrangian equations are as follows:
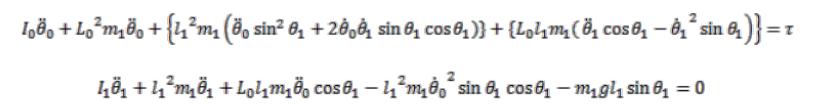
So, we had created a function for the dynamic equations where in we have 4 equations.
Animation
For the animation part, we tried to create a 3D visualization of the Inverted Pendulum, for which, we used plot3 function which helps create a line in 3D. Then, moving ahead with the systems, we achieved an ideal system as well as a system controlled using LQR(Linear Quadratic Regulator).
Simulation of the two different systems
-
For an ideal inverted pendulum system, the external input provided should be zero. Visualization of ideal inverted pendulum :
- Initial point: [pi 0 pi/2 0]
-
For LQR system, we found out the jacobians A and B. Then, using the inbuilt function of LQR , value of K is found out. Visualization of inverted pendulum using LQR :
- Initial point: [pi 0 pi/6 0]
- Final point: [0 0 0 0]
Problems we faced!
Deriving the equations was the major hurdle in our simulation step. So, we had to refer multiple research papers for it. Even though we went through multiple papers, yet the equation satisfying our conditions was not found. So we deployed a large amount of time towards obtaining the required equations. Still after deriving the equation we had to give MATLAB a jacobian, from which it shall calculate the position and by using LQR stabilised our system. We faced issues in this step too. Even though there is function in MATLAB itself to help us find the jacobian, but the input equations must be properly correct and in order. Many times our variables were not in proper position or there were syntax errors. As the stable points are [0 0 0 0], we used subs function to substitute that in our equations before calculating the jacobians as the state variables present in the jacobian was causing errors in the program. We obtained two jacobians A and B, which were calculated with respect to our setpoints and the input vector, u, respectively. We also faced errors while running the program, for which, our mentor helped us in debugging them. We also referred to documentations in this regard.
Future Tasks
Next, we will build a LED blink project on ESP 32 and then controlling DC motors using the same. We will also learn about quadrature encoder that shall help us in our project.